This page hopes to debunk a particular numerologist's claim that I heard explained recently. The claim centers around assigning each letter of the alphabet a number, the number of its position in the sequence of letters that we say when we sing the alphabet song. A=1, B=2, C=3, and so on.
I have about 70 thousand words in my English dictionary with an average word's length of eight letters. For our crude proposes, let us assume that a random letter chosen from a dictionary word will on average fall in the middle of the alphabet. From this, we can multiply the number of letters of the average word with the middle position of 26 letters, and get 8 × 13 = 104. That is to say, with a completely random, meaningless distribution of about eight letters, on average the sum will be about 104. With a little knowledge of statistics, we can predict that the probability of number for random words will trace (roughly) a bell-curve, centered about 104.
So we have a hypothesis, now we need to prove it. I wrote a program to calculate the values for all the English words and write each word to its value's file. All words with value "42" got written to file "042.txt", for instance. I then plotted the number of words in each file on the Y axis and the number of the file on the X axis.
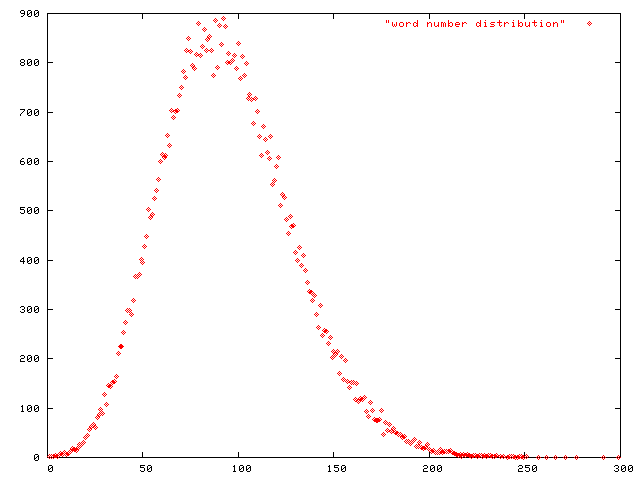
Surprise! A bell-curve.
(It's not perfectly centered at 104, but we made some assumptions that are probably off by a few percent, like the frequency distribution of letters and their alphabet order, the not-symmetrical graph of word lengths, and many others surely. Note that there is no upper limit on a word's value, but there is a lower limit, "1". These factors are almost insignificant, so we needn't clutter the discussion with their inclusion.)
Now, let's think about what this graph shows us. Almost all words have values from 1 to about 200. Another way to say that is: Almost all of the seventy thousand words can be sorted into about 200 boxes. The boxes in the middle will have the lion's share of the words, as the middle of 1 to 200 about where the "104" box is.
With all this information, think of a favorite number. If you want to associate your favorite number with a word, you need only look in that number's file and pick one.
If you're like many people whose favorite number is too low to be in this list of files, you're out of luck using this straightforward, albeit arbitrary (because the order of letters in the alphabet is itself arbitrary) scheme. To get to the number you want, since the gods didn't see fit to include your favorite number, you have to alter the results in some way, perhaps to change the enumeration. You could multiply every enumerated value by some value, but beware the the number you choose heavily influences which lists your words will be in: You have to choose a multiplier that is a factor of your goal number. When you multiply the enumeration by X, every word sum is going to be divisible by X.
A common favorite number among Christian-inspired numerologists is "666", so you could choose factors of "666" (2, 3, 37, or any multiplied combination thereof) to multiply the filenames' numbers by, to find words that match.
The smart numerologist is best served by choosing factors that sum to find a list around the peak of that bell-curve, so he gets a large list of words to sound spooky about.
The likelihood that a word will appear in any particular bucket appears to be completely arbitrary, and if you have to choose a number with which to multiply the enumeration, then you must realize that multiplying arbitrariness by arbitrariness can yield anything you might fancy. You have constructed a system custom-designed to find what you're looking for, so you shouldn't be surprised when you find it.
Related reading:
The numbered files are words of a particular value, whereas "values_by_word.txt" is a list of all words and their values.